Tacos For (almost) Everyone

Do you remember when I blogged about the Ultimate Task for Vertical Planning: Stacking Cups? If not, feel free to check it out at your convenience. I've got another task for you that can be used at multiple grade levels: Dan Meyer's Taco Cart.

When asking:

Who will reach the taco cart first?

there are so many mathematical opportunities awaiting us. Here are a few:

Math 6 (maybe Math 7)
Pass out this handout during Act 2 and tell students you will only give them one dimension. Choose wisely.

Read more about this great technique on Fawn's blog post about Mr. Meyer's Taco Cart.
It simply is brilliant. Students are measuring the dimensions (distances) on the paper and using proportional reasoning to figure out the real life distances. I recommend students use centimeters when measuring the dimensions of the triangle on the handout. I really enjoy this technique.

Math 8
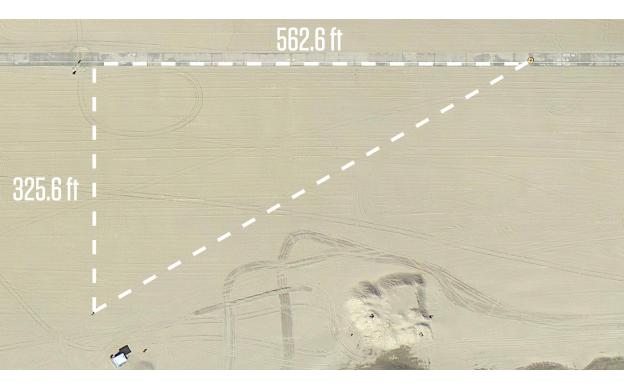
If you're a math teacher and you see the picture Dan provided for Act 2, your intuition will most likely steer you in the direction of the Pythagorean Theorem. Go for it!

Geometry (HS)
Let's say you have already used Taco Cart during the year to apply the Pythagorean Theorem or Distance Formula (Desmos). How about we extend the mathematics and look for more right triangle relationships in Taco Cart. I noticed that the hypotenuse is about twice the length of the shorter leg. Let me connect that to the context of the story: Ben's distance is about twice the distance Dan travels in sand. That's right, Dan gave us a 30-60-90 right triangle. Pro skills there, Dan.
*I'm not saying the 30-60-90 relationship is the most intuitive, but we'd be helping students make connections with previous learning. 

Algebra and Beyond
As you move into the sequels provided on the website, there's a lot of higher level math. Depending on the question, the problem-solving is fun. I worked with a high school group of math teachers who found it extremely challenging to solve the question:

What path to the taco cart would take the least amount of time?

Overall, this is such a fun and meaningful task. Dan has given us a treat! Today, my students did such a great job arguing, sharing theories, identifying variables, and using their intuition even before I unveiled any information from Act 2. It was awesome! I'm avoiding the use of the Pythagorean Theorem this round. I went Fawn-style by giving students only one dimension on their Act 2 handout. So good!

Tacos por favor,
942